3.   TYPES (Part 1)

This chapter addresses the data type facility for the RED language. The use of the various type features is explained and illustrated, the major issues underlying the design decisions are discussed, and alternative approaches are compared.

Section 3.1 presents the notions of type and subtype and analyzes a set of implementation techniques which can be used for code optimization.

Section 3.2 examines the type equivalence issue and justifies the approach taken by RED.

Section 3.3 discusses the "type opacity" question: when a type is declared in terms of an underlying type, what is the relationship between the two? Literals and constructors are also described here.

Section 3.4 covers a variety of issues concerning the predefined RED types BOOL, INT, and FLOAT, and explains why no fixed point facility was included.

Section 3.5 discusses a number of topics connected with enumeration types.

Section 3.6 addresses the design decisions relevant to aggregate types (arrays, records, unions, strings, sets).

Finally, Section 3.7 is concerned with indirect (i.e., "pointer") types, their use, and their implementation.

3.1  THE NOTIONS OF TYPE AND SUBTYPE


3.1.1  BASIC CONCEPTS

One of the most troublesome errors in assembly language programming is to apply to a data item an operation inappropriate to the way the data should be used. For example, treating an integer bit pattern as though it were an address (or even an instruction); treating a floating point bit pattern as though it were a sequence of characters. With the development of High Order Languages has come an understanding that the best way to prevent such errors is via "strong typing" (SM 3A); that is, a program's data are partitioned into (disjoint) categories called types and only such operations may be applied to a data item as are consistent with its type.

In many cases, however, the notion of "type" is not sufficiently restrictive. To illustrate this point, we consider the integer data type (INT, in RED). In the interest of portability, readability and efficiency, Steelman 3-1C requires that the lower and upper bounds of each INT variable be specified explicitly by the programmer. These range bounds cannot be considered to be part of the type -- i.e., it would be incorrect for the language to define lNT(i..j) as a type -- for two reasons:

1. The bounds may be run-time determinable (3-1C), whereas the type must be known at translation time (3A).

2. It must be possible to write an assignment statement where source and destination have different ranges, without requiring an explicit conversion (3-1C), but implicit conversions between types are prohibited (3B).

Range bounds do not define new types, but rather serve to constrain the value space of the (single) INT type and are called attributes associated with the INT type. A type, together with values for its attributes, is called a subtype. Thus INT(l..10) and INT(-i..i) are INT subtypes, denoting the integer ranges 1,2,...,10 and -1,...-1,0,1,...i, respectively.

In RED, the notion of subtype applies uniformly to all types, whether built-in or user-defined. A subtype must be specified for each variable at the time of its allocation and cannot be changed during the lifetime of the variable. The values for attributes may be computed at run-time and interrogated via a "dot qualification" form. Either a subtype or a type may be specified at the declaration of a formal parameter to a routine. Allowing a type with no subtype constraints to appear in such contexts is extremely useful (and is, in fact, required by SM 7G); e.g., a WRITE procedure must be able to output INT values from arbitrary INT subtypes.

The requirement in RED that subtype constraints be specified for variables is somewhat stronger than is necessary to satisfy SM 3D which states that "the value of a subtype constraint for a variable may be specified when the variable is declared." We adopted the more restrictive (but uniform) rule in the interest of language simplicity, readability, and efficiency. Note, however, that subtype constraints are not necessary when a constant is declared. That is, the user may simply declare

      CONST message := "MANUAL INTERVENTION REQUIRED";

instead of counting characters as in

      CONST message : STRING[ASCII](28) := "MANUAL INTERVENTION REQUIRED";

As an illustration of the principles of type and subtype, it is straightforward to write a function which finds the maximum value in an array of FLOATs

and to invoke the function on actual arrays of FLOATs:

Note that the following attempted declarations are illegal:

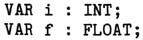
since subtype specifications are required for variable declarations.

A dot qualification form is used to interrogate the values of attributes, with the attribute name used as the selector. This convention applies uniformly across all types, built-in and user-defined. Thus, with the declarations

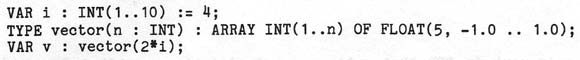
we have i.MIN=1 and i.MAX:1O (MIN and MAX denote the bounds attributes for INT data), and v.n:8 (the formal parameter identifiers in type declarations denote the attributes associated with user-defined types). The same notation was chosen for both attribute inquiry and record component selection, since conceptually the user can regard a data item as though it were a record comprising the values for the attributes (constant for the lifetime of the data item) and a data value (modifiable if the data item is a variable). We emphasize that in practice it is not always necessary to store the values for attributes at run-time; this issue is discussed in the next section.

3.1.2  IMPLEMENTATION ALTERNATIVES


Avoiding Run-Time "Dope Vectors"

A data item has a type (known at translation time) and a set of values for the attributes associated with the type (in general, not known until run time). A natural implementation is to store the subtype information -- the values for the attributes -- at run time along with the data value (e.g., in a "dope vector").¹ A typical case where this would occur is array data. If a routine has a formal parameter which is, say, an ARRAY INT OF BOOL, then the lower and upper bounds of the array index can be passed at run time with the actual parameter to each invocation of the routine.

This does not imply that such "dope vector" information must always be stored at run time; there are important cases where the translator can effect considerable efficiency by maintaining subtype information at compile time. For example, if the user declares

      VAR x : 1NT(1..8);

then the translator can keep track of the bounds values for x. Suppose that x is passed as an actual parameter to a routine R which expects a formal parameter f of subtype INT(m..n) where m and n are manifest. (The bounds of f can also be maintained by the translator.) Independent of the binding class for f, no run-time dope vector is needed for x:

1. In the case of VAR or READONLY, the translator can check the validity of the invocation R(x); the subtypes must be identical.

2. With the other bindings, a run-time check may be necessary to ensure that x is in the range m..n (before entry to R, when f is CONST), or that f is in the range 1..8 (after exit from R, when f is OUT). The array bounds, however, need not be stored with either the actual or the formal parameter at run time.

If m or n is not manifest, then the translator can generate code which first produces a dope vector for x comprising 1 and 8, and then passes as the actual parameter the dope vector together with the value of x. Thus the dope vector need _ only be generated when it is required.

What does the translator do if the formal parameter is specified simply with a type (INT) and not a subtype? In this case it can certainly take the second approach mentioned above and generate the dope vector at the point of invocation. If it is important to conserve storage for the executable code bodies, at the possible expense of data storage and execution time, then such an approach can be adopted. There are, however, two alternative techniques which can be employed. First, the translator can regard the routine as though it were generic with respect to the subtype of the formal parameter (it might adopt such an approach if the routine contains the INLINE pragmat). For example, given the declaration

      PROC p(f : INT); ... END PROC p;

the translator can produce separate versions of p for each different manifest subtype of the actual parameters to invocations of p; if p is invoked with an actual parameter whose subtype is not manifest, then an instance of p can be generated which expects the range bounds of its formal parameter in a run-time dope vector.

As a second approach, the translator can avoid passing "dope vector" information without relying on such expansion. The main point is that if the attributes of a routine's formal parameter are not interrogated (directly or indirectly) from the routine, then there is no need to store the values for these attributes with the actual parameter when the routine is invoked. This is a particularly useful optimization for CONST and READONLY parameters, especially for attributes such as range which are relevant only for the target of an assignment and which are thus not likely to be interrogated. In the above example, if the MIN and MAX attributes of f are never used, then the range bounds for x need not be passed at the invocation D(x) -- even when these bounds are not manifest. Note that, to perform this optimization, the translator must check if f is passed as an actual parameter to a routine which interrogates its formal parameter's attributes, etc.

Types Supporting Multiple Representations

As a general principle of language design, it is advisable to constrain data types to single representations. In fact, one of the changes from Ironman to Steelman was the deletion of the requirement that the language support multiple representations per type. The basic problem with multiple representations is that efficiency may be sacrificed (via run-time code to perform conversions between representations) without the programmer's knowledge.

Although the full generality of multiple representations per type is not justified, there are some important special cases where efficiency can be gained, rather than lost, when the translator implements the same type under different storage schemes. The two most frequent cases are INT and FLOAT, since many machine architectures support integer data of different lengths (e.g., halfword, word, doubleword) and floating point data of different precisions (e.g., single and double).( The implementation issue may be summarized as follows: how can the translator select the smallest storage unit compatible with the declaration of a data item, and how can a routine be compiled if a formal parameter is specified with type (rather than subtype)? For ease of exposition, we treat the INT and FLOAT cases separately.

The selection of a storage unit for an INT variable can proceed as follows:

1. When the range bounds are known at translation time, the minimum storage unit which can support that range may be chosen.

2. When the range bounds are determined at run time, it will frequently be the case that the bounds of the range bounds are known at translation time. For example, given the declarations

   

   the translator can determine that the maximal range for x is INT(m.min .. n.max); i.e., INT(0..1000). Thus the minimal storage unit supporting this range can be chosen. (Note that the actual range m..n is still used for checking on assignments to x; the bounds m and n will in general be stored at run-time).

3. When the range bounds are determined at run time but the approach of case (2) is inapplicable, the translator can choose a storage unit consistent with its efficiency considerations. In particular, it need not make "worst case" assumptions; e.g., it may adopt full-word integers as the standard representation and provide double-word representations only when manifest bounds require them.

The preceding discussion focused on the translator's choice of a storage unit for an INT variable based on the subtype information specified for it. what happens when a formal INT parameter is declared and no subtype information is present, either on the formal parameter or through ASSERTions? One approach is to treat the . (routine as though it were generic with respect to subtype, as discussed earlier in connection with dope vector avoidance. Alternatively, the translator can treat the routine as though it were generic with respect to the representation. That is, each invocation of the routine passes an INT of some particular representation (halfword, word, doubleword), and a body for the routine can be compiled with the formal parameter having the same storage unit as the actual. For example, if x and y are halfword INTs, x+y could be compiled into halfword arithmetic; if they are full-word INTs, full-word arithmetic code would be generated. It is important to note in this regard that the language does not guarantee a unique maximal range for the results of arithmetic operations; this allows the implementation to produce either a halfword, fullword, or doubleword as the result of x+y, based on the sizes of the operands and the size of the target for the result. Note also that if the translator chooses the above approach and treats a routine with a formal INT parameter as though it were generic with respect to representation, then it may perform the analysis described earlier to avoid passing subtype information at run time. That is, if the attributes of the parameter are not interrogated (directly or indirectly) by the invoked routine, they need not be passed at run time.

The implementation of multiple representations for the FLOAT type is analogous to INT, with respect to both the selection of storage size and the translation of routines taking formal FLOAT parameters with no subtype information.

The determination of storage size is actually somewhat easier in the case of FLOAT than with INT, since the specified precision when a FLOAT variable is declared must be manifest (SM 3-1D). Thus the translator can choose a storage size (and actual precision) large enough to support the specified precision, subject to a target-machine dependent limit (e.g., double precision).

When a routine is declared with one or more formal FLOAT parameters lacking subtype information, the translator has considerable flexibility regarding implementation. At one extreme, the translator may represent all FLOAT data at maximal actual precision and pass the subtype information (specified precision, range bounds) as part of a run-time dope vector. This minimizes the number of code bodies at the expense of run-time data storage and execution. Although clearly unacceptable in production environments, such a strategy may be appropriate for "debugging" translators, where speed of translation rather than object code efficiency is important. At the other extreme, the translator may treat the routine as though it were generic with respect to subtype. Thus the routine would have a separate instantiation for each different manifest subtype of_actual parameters in invocations, as well as instantiations which expect the range bounds in a dope vector. For example, if x and y were declared to be of subtypes FLOAT(4, 0.0 .. 1.0) and FLOAT(8, -10.0 .. 10.0) then the translator could produce code for x+y which was tailored to these subtypes, taking into account that x has single precision and y has double precision. This strategy conserves execution time and data space at the expense of code space.

In practice, we expect a production-quality translator to take a compromise position between these extremes and in the process generate efficient run-time code without proliferating code bodies. In particular, the following strategy is recommended:

1. Treat routines as generic with respect to specified precision but not with respect to range. Thus, with the above example, code for x+y could be tailored to precisions 4 and 8.

2. To avoid passing range bounds at run time, the techniques discussed earlier in this section can be employed. For example, since the "+" routine does not require the range bounds of its actual parameters (just a knowledge of the precisions is sufficient), there is no need to pass these at run-time.

Note that in many cases the translator can optimize code space by treating a FLOAT routine as though it were generic with respect to actual (instead of specified) precision. In particular, if the specified precision of the formal parameter is not interrogated (directly or indirectly) in the routine, then such an optimization can be employed. For example, suppose that the user declares the following square root function:

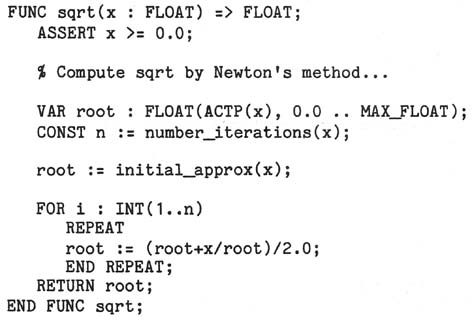
Provided that the routines to which x is passed as an actual parameter (number_iterations, initial_approx, "/") do not interrogate the specified precision of their formal parameters, the translator can produce just two versions of sqrt -- one for single precision and one for double -- without passing specified precision at run-time.

Use of Type Declarations

In the preceding discussion we have looked at techniques which the translator can use to implement subtypes efficiently. It should be noted that the programmer can directly effect the production of efficient code, at the sacrifice of some generality, by turning "subtype" information into "type" information. Specifically, this allows the translator to avoid storing such information at run time, since it must be manifest and will be the same for each object of the type. The following example shows how specified precision can thus be made to distinguish type:

Summary

In this section we have addressed the main issues concerning the implementation of subtypes, focusing particularly upon techniques for maintaining and interrogating subtype information at translation time instead of run time. The basic strategy is for the translator to apply the same techniques which are used in the implementation of the generic facility. An analysis of the application of these methods to two important cases, the INT and FLOAT types, demonstrated how the translator can produce efficient object code and take advantage of target-machine specific storage representations.

3.2  TYPE EQUIVALENCE


3.2.1  INTRODUCTION

In a strongly typed language, one of the most important issues which must be addressed is that of type equivalence²; i.e., when are two data items considered to have the same type? The language rules in this area have major impact on the usability, readability, simplicity, and efficiency of programs. In this section we discuss the alternatives which were considered for type equivalence in RED, and justify the decision which we made.) In summary, two type invocations in RED denote the same type provided that their names are lexically identical, where a name is obtained by expanding all abbreviations (if any) and then removing all "round-bracketed" information. Type equivalence can always be checked at translation time.

For example, with the data declarations

the types of x, y, and z are RECORD[a : INT, b : INT], RECORD[c : INT, d : INT], and RECORD[a : INT, b : INT], respectively. Thus x and z have the same type, which is distinct from the type of y.

The rules for type identity must take into account built-in types (such as BOOL, INT, FLOAT), generated types (such as enumeration, record, array, union, and indirect types), and new (i.e., user-defined) types. Moreover, the rules must be consistent with the language conventions for type opacity; this implies that the declaration of an ABBREViation does not introduce a new type, whereas the declaration of a type does. Four alternative approaches were considered with respect to type identity, which we will denote by the terms "pure name equivalence", "structural equivalence", "single-instance generators", and "extended name equivalence". The approaches differ primarily with respect to rules regarding the equivalence of generated types.

3.2.2  PURE NAME EQUIVALENCE

The pure name equivalence approach simplifies the problem of type identity by eliminating those cases which can cause complications. Under this scheme, it would be illegal to invoke generated types except in the definition of new types. That is, the attempted declaration

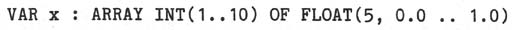
would be illegal, and the user would have to define a new type before declaring x; e.g.,

The question of type identity would then be resolved simply by checking type identifiers for lexical identity. (Two identifiers are considered "lexically identical" if they are textually identical and correspond to the same declaration.)

This approach is basically that proposed for the Phase 1 RED language [Br78]. Its main disadvantage is that it introduces into programs a proliferation of type names, many of which are only used once, with a resulting loss of readability. Additionally, it interacts badly with subarray selection: with the type and variable declarations for x_type and x given above, it is not clear what the type of x(2..5) should be. As a result of these drawbacks, the pure name equivalence approach was rejected.

3.2.3  STRUCTURAL EQUIVALENCE

At the opposite extreme from pure name equivalence, the structural equivalence approach allows maximal freedom in determining type identity for generated types. Stated somewhat loosely, any two invocations of the same generator would produce the same type provided that their component types are the same. The following examples illustrate the intent of this rule:

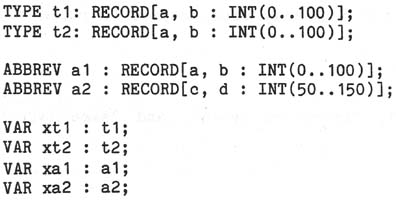
Variables xt1 and xt2 would have different types -- t1 and t2 -- whereas xa1 and xa2 would have the same type -- RECORD[INT,INT].

With the structural equivalence strategy, two enumeration types would be the same if they comprise the same elements in the same order, and two array types would be the same if their corresponding index types and component types are the same. The rules for union types would be the same as for record types; field names are not relevant with respect to type identity.

Problems with structural equivalence arise primarily in connection with indirect types. First, the presence of cycles in ABBREViation declarations would make it difficult for the reader to decide when two types are the same. Consider the examples

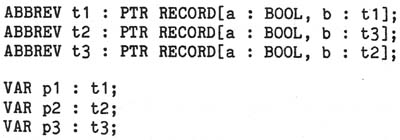
Do p1, p2, and p3 have the same type? Kieburtz et al; [KBH76] state a rule which implies an affirmative answer: two indirect types "are judged equivalent if they are alleged to be equivalent, and the allegation is not disproved by a structural equivalence test upon the types pointed to." However, the formulation of a recursive algorithm to solve the problem does not eliminate the confusion that readers of the program are likely to feel.

The second problem with structural equivalence concerns the role of subtype information in indirect types and arises when "anonymous" indirect types are allowed (e.g., on data declarations). Suppose that the user intends to declare a variable which is constrained to point to a string of a given fixed length. For example,

The assignment x2 :: x1 should not be permitted. (If it were, then either the length information from x1 would be inherited by x2, conflicting with the declaration of x2 which constrains the length to 10, or a subsequent assignment such as x2(8) :: x2(1) could modify the contents of an arbitrary location in memory.) The assignment x2 := x3 should be permitted only if n = 10. Thus, x1, x2, and x3 would have the same type -- PTR STRING[ASClI] -- and subtype constraints 7, 10, and n which are checked on assignment and parameter passing. Consider now, however, the case where a variable is intended to point to strings of arbitrary length. One possible syntax would be

The type of x4 is PTR STRING[ASCII], but the notion of the subtype of x4 is not so clear, since x4 can be used more freely as the target of an assignment than can x1, x2, or x3. If anonymous indirect types are permitted, as implied by the structural equivalence approach, special rules would be needed in the language to explain the role of subtypes for indirect types.

An additional problem with structural equivalence concerns the role of field identifiers in record and union types. If the field identifiers are not relevant with respect to type identity, then in the following example

z and p would have the same type, which was probably not the programmer's intent. Although this problem could be solved with a suitable rephrasing of the language rules, the difficulties intrinsic to structural equivalence when anonymous indirect types are allowed have caused us to reject this approach to type identity.

3.2.4  SINGLE-INSTANCE GENERATORS

One possible compromise between the extremes of pure name equivalence and structural equivalence is for each invocation of a type generator to produce a separate type, even when the invocations are lexically identical. This approach will be called that of "single-instance generators". For example, consider

Since INT is a type (not a type generator), i1 and i2 would have the same type.

However, e1 and e2 would have different types (ENUM is a type generator); r1 and r2 would have the same type, different from the type of r3.

Although reasonably simple to implement, the single-instance generator approach detracts from the ease with which the language could be learned and used.

1. A semantically significant distinction is made between a type and a type generator, but in practice it is not so easy to remember into which category a given candidate falls. For example, there is no intuitive reason to regard enumeration types as instances of type generators; given the analog to integers with respect to range specifications, one might expect that e1 and e2 above should have the same type. In the case of user-defined (or library-provided) types the issue is more subtle. For example, does FILE[INT(O..100)] produce a new type every time it is invoked?

2. The interaction with ABBREViations can lead to confusion. If the user declares

   ABBREV color_type : ENUM['red, 'yellow, 'green, 'blue];

   

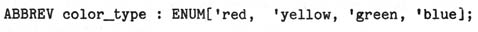
   then the semantics of

   

   must be explained (and learned) very carefully. In particular, the abbreviations cannot simply be expanded lexically (as one might expect), since this would imply that c1 and c2 have different types.

3. Type generators become useless on formal parameter specifications, since no actual parameter (except possibly a constructor whose type was ambiguous) could ever have the same type as the formal. For example, though it might be useful to have a procedure which sorted arbitrary arrays of floating point values, the straightforward approach of declaring

   

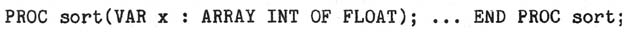
   would not work, since the type of the formal parameter x would be a different type from all other ARRAY INT OF FLOAT types.

4. The fact that

   

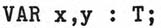
   would sometimes be equivalent to

   

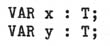
   (when T is a type), and sometimes not (when T is an invocation of a type generator) is anomalous.

5. It would become very clumsy to refer (in comments or informal discourse) to the type of an object. Given the declaration

   

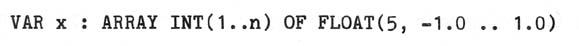
   how does one describe the type of x? The denotation "ARRAY INT OF FLOAT" would be incorrect, since this denotes a new type, distinct from that of x.

6. The semantics of array slicing would be somewhat confusing. Given the declarations

   

   what is the type of x(1..3)? Which of the following assignments is legal?

   

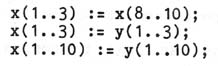
   The above problems have caused us to reject the single-instance generator approach to type equivalence. Though some of these difficulties could be avoided by the user's declaring new types instead of using anonymous generators, this would reduce the approach to (and thus result in the drawbacks of) the pure name equivalence scheme discussed earlier.

   
   
   
   3.2.5  EXTENDED NAME EQUIVALENCE
   
   Extended name equivalence represents a compromise between pure name equivalence and structural equivalence- which avoids the anomalies of the single-instance generators approach. The following are the essential attributes of extended name equivalence.

   1. Anonymous (and abbreviated) indirect types are prohibited. Thus, if one intends to use an indirect type, a new type must be declared.

   2. A game is derived from a type invocation by expanding all ABBREViations and comma-separated field lists, and then removing all "round-bracketed" information.

   3. Two type invocations yield the same type provided that their resulting names are lexically identical.

   These rules apply consistently to built-in, generated, and user-defined types, as illustrated by the following examples:

   

   The extended name equivalence approach was adopted for the RED language because it provides intuitively reasonable semantics without dictating a particular programming style, and because it meshes well with the language's approach to types and subtypes. It has an advantage over pure name equivalence in allowing anonymous enumeration, array, record, and union types. It has an advantage over structural equivalence in avoiding the non-intuitive semantics of anonymous indirect types and in treating field identifiers as relevant to type identity. And it has an advantage over single-instance generators in avoiding the variety of anomalous behaviors described above.

   ***********

   1 Note that "dope vector" information need not be stored contiguously with the data. Thus several data items of the same subtype could share the same dope vector.

   2 The terms "equivalent types", "identical types", and "same types" are used interchangeably.