8.   OVERLOADING AND GENERIC DEFINITIONS

8.1  OVERLOADING

In accordance with SM 7A, RED permits routines to be overloaded. Such a facility is useful because it permits a single name to be given a standard meaning that transcends type boundaries. For example the name "+" can be chosen to mean addition. Addition is an action that is relevant to many types; e.g., integers, reals, vectors, matrices, etc. Overloading permits many definitions of + to be given. These definitions will be distinguished by the types of their actual parameters (i.e., they will have different signatures); also, they will have different bodies that perform the addition operation in accordance with the semantics of the corresponding types.

All typed languages provide a certain degree of overloading. At the very least, operations like + are overloaded for built-in types. In languages with user- defined abstract types, some means of permitting two types to have the same operation is required.

In RED, the declaration and invocation of an overloaded routine have the same form as for a non-overloaded routine, and the selection of the invoked routine is done in a simple manner. Furthermore, selection can always be done at translation time, since it is based on type information.

Various issues associated with overloading are discussed below. We will use the term "overloaded definition" to mean the declaration that overloads some routine name, and the term "use form" to mean the form that is used to invoke the overloaded routine.

In the interest of language consistency, RED does not restrict overloading to routines. For example, tasks and routines are quite similar; they are the deferred units invoked for their actions. To permit overloading for routines and not tasks would make an artificial distinction between them. Thus, overloading of tasks is allowed. Moreover, overloaded ABBREViations are useful. in dealing with related types and subtypes. This is particularly true in the case of enumeration types; e.g., the built-in ASCII ABBREViation is overloaded so that it may be used either as a type or as a subtype (in the former case it may be invoked with range bounds to yield a subtype, such as ASCII('A..'Z)). As a result of these considerations, RED permits any deferred declaration (other than a type declaration) to be overloaded. (Note that it is not possible to allow overloading of types, because of the potential ambiguity regarding the underlying type.)

Overloading can be produced by explicitly providing several definitions of the same name, or by means of a generic definition. In this section, only explicit overloading is discussed; generic overloading is discussed below in Section 8.2.

8.1.1  PROVIDING OVERLOADED DEFINITIONS

In RED, overloaded definitions are introduced as needed. For example, when a new abstract type is defined, some of the operations in the capsule defining the new type may be overloaded definitions. In the course of using the type, the programmer may provide further overloaded definitions. For example, if no "print" operation was provided in the capsule defining abstract type t, a programmer using t may, provide such a definition.

Overloaded definitions appear in the program text when it is convenient to introduce them. This is in contrast to ECL [Ha74] and PL/I, where it is necessary to provide "overload lines" in the single definition of the overloaded routine. The method in RED provides much better modularity.

8.1.2  LEGALITY OF OVERLOADED DEFINITIONS

When an overload use is processed to select an overloaded definition, it should not be the case that more than one overloaded definition could be selected. Such a situation must be considered an error: the alternative of having the translator make an arbitrary selection among the possibilities would certainly have a negative impact on readability and understandability. Furthermore, it is desirable that the error be detected at the time the overloaded definitions are translated rather than when they are used. This permits error detection to occur as early as possible, and also in the proper context, since it is really the definitions, and not the uses, that are in error.

RED satisfies these objectives by requiring that all overloaded definitions local to a scope must not conflict with one another. Two overloaded definitions conflict if their signatures are equal and their translation-time properties (if any) are equal. Recall that signatures describe the order and types of the formal parameters. Translation-time properties are described below, in Section 8.2.2. Since only types and not subtypes are involved, conflict between overloaded definitions can be detected at the time the overloaded definitions are translated.

8.1.3  SELECTING THE OVERLOADED DEFINITION

When the translator processes an invocation; e.g., "READ(a)", or "x+y", it determines the signature of the invocation, and selects the overloaded definition that has that signature. Note that:

1. There is no need to resolve ambiguity in selection, since conflicting overloaded definitions are a translation-time error. (The problem of ambiguous literals and constructors is addressed in Section 3.3.4.)

2. The selection can be done at translation time, since only types are involved.

More general selection rules can easily be imagined. For example, for an overloaded function, the result type could also be considered part of the signature. However, this leads to problems. For example, suppose f and g both have two (conflicting) overloaded definitions:

      FUNC g(x:INT) => INT;
      FUNC g(x:INT) => BOOL;
      FUNC f(x:BOOL) => BOOL;
      FUNC f(x:INT) => BOOL;

These definitions would not conflict if the result type were considered part of the signature. However, the invocation f(g(x)) does not unambiguously correspond to specific definitions of f and g. It is to avoid such problems that the result type is not included in the signature.

8.2  GENERIC DEFINITIONS

Generic definitions are a way of providing many definitions with a single form. Generic definitions have generic parameters; these differ from ordinary parameters in that the actuals must have values that are manifest. Furthermore, actual generic parameters are passed at translation time as compared to ordinary actual parameters, which are passed at run time. The generic provides a separate definition for every possible combination of actual generic parameters; since these parameters are manifest, the definitions can be produced at translation time.

Generic definitions can be given for each of the deferred units: procedures, functions, tasks, capsules, types, and abbreviations. Generic definitions are used when a class of definitions ranging over many types is wanted, or when a routine or task parameter is needed.

8.2.1  MAJOR TECHNICAL ISSUES

The major technical issues are the following: what is a legal generic E definition, what definitions does it produce, and when are they produced. At first consideration, it may appear that generics should simply provide a macro facility; i.e., that the names of the actuals should be substituted for the formals to obtain an instantiation of the macro; this instantiation would then be translated in the using environment.

However, careful study of a macro facility reveals some difficulties. The most serious of these is the lack of a definition environment. For example, suppose that a generic definition contains an invocation of a routine f to achieve a certain effect. with macro-like semantics it would be impossible for the definer of the generic to guarantee that the proper f will be invoked. Since the meaning of the generic definition is dependent upon the routines it invokes, it would be impossible for the definer of the generic to ensure that its intended meaning is realized. Therefore the macro approach is not acceptable; it conflicts directly with the higher level goal of modular program construction.

Generics in RED have aspects of both routines and macros. Like routines, a definition environment supplies the interpretation of all non-local identifiers. Also like routines, the values of actual parameters (not the names) are passed. However, generics resemble macros in that they are instantiated at translation time to produce the actual entity that is used at run time. Instantiation can occur at translation time because all the actuals are manifest.

Meaning of a Generic Definition

A generic definition comprises a set of generic parameters, an optional NEEDS list (see Section 8.2.3), and a declaration of a deferred unit. It can be thought of as providing an instance of the deferred declaration for all possible values that the formal generic parameters can assume. For ease of exposition, we will call the deferred declaration the "body" of the generic definition.

For example, consider the generic definition

This definition provides a function declaration for r[i,f] for every integer value i in the range 1..10 and function f from FLOAT to FLOAT.

Of course, it would be inappropriate to produce all instantiations at the time the generic definition is processed by the translator, since few of those instantiations would actually be used. In fact, it would be impossible to produce all instantiations, since the translator does not know all possible functions from FLOAT to FLOAT. Instead, the instantiations are produced when they are needed.

One possibility, similar to macros, would be to require an explicit form that instantiates a generic. Such a requirement would simplify the translator's job somewhat, but it would complicate the use of generics and result in the introduction of superfluous names by requiring the user to name each different instantiation. Therefore, we do not require explicit instantiation. In fact, it is transparent to the user whether a generic or a non-generic construct is being invoked. The first time a generic is used with particular actual values, the instantiation is actually constructed. When the generic is used with those values subsequently, the instantiation can be constructed again, or the previously constructed instantiation may be used. In the latter case, the translator must keep track of previously constructed instantiations. An instantiation can be named by the identifier that names the deferred unit, together with the values of the actual generic parameters. During instantiation, the generic formal parameters are given the values of the actual parameters in the environment of the instantiation. Then the deferred unit that is the body of the generic is translated in the defining environment. It is useful for some names in the generic to be bound in the instantiating environment; the NEEDS list fulfills this purpose.

Legality of Generic Definitions

The specification of a (formal) generic parameter includes a generic constraint. Uses of the formal generic parameter within the deferred declaration must be consistent with the constraint, and actual generic parameters supplied to instantiations must likewise satisfy the constraint. Thus generic constraints on formal generic parameters are analogous to type specifications on formal parameters to deferred units.

Actual generic parameters may be types, subtypes, routines, tasks, and manifest values, as required by Steelman (SM 12D). As an example, the following generic function performs numerical integration by Simpson's method:

The RED rules about legality of generics define the interface of the generic as fully as possible. The interface information constrains both the generic definition and its use. The use must provide actual generic parameters that satisfy the constraints, while the definition can only use the parameters in ways consistent with the constraints. For example, inside integrate, f must be used as a function from FLOAT to FLOAT; the user of integrate must provide such a function. Of course, only syntactic information can be captured in our interface description. Semantic restrictions, such as assumptions in integrate about the meaning of f, cannot be described or enforced; such a step requires a program verifier, not a translator.

8.2.2  OVERLOADING VIA GENERICS

Overloading definitions of a routine or task can be provided explicitly by writing different definitions (as discussed in Section 8.1), or implicitly by means of a generic definition. In either case, the overloaded definitions may not conflict. In the case of generic overloading, this means that for any routine or task name, and for any legal actual translation time property list associated with that name, there must only be one definition local to the definition scope with any given signature. The translation-time property list is specified through square brackets after the name; e.g.,

states that integrate has a single translation-time property. This generic definition provides a definition of integrate for any legal value of f (i.e., any function from FLOAT to FLOAT). Each such definition of integrate has signature FLOAT, FLOAT, INT. However, the definitions do not conflict with each other, since each has a different actual translation time property. The value for the actual generic property is supplied whenever integrate is used; e.g.,

      x:= integrate[sin](x, y)

A generic definition could produce routine or task definitions that conflict with other definitions, external to the generic but local to the scope containing the generic. There is no way that a generic could produce overloaded declarations that conflict with one another if we require that all generic parameters appear in the generic property list. This is, in fact, the requirement for non-overloadable deferred units such as capsules and types. However, we have weakened the rules for tasks and routines to enhance usability.

It is often the case that a generic parameter determines the type (or subtype) of a routine parameter. When this happens, the generic parameter can be derived from the actual routine parameter. For example, consider

A legal use of p is

      VAR y: INT(1..10);
      p[INT] (y);

However, such a form requires useless redundancy: the actual translation time property can only be the type of the actual parameter. No additional information is gained by requiring the user to explicitly state the actual generic property in this case, but the possibility of errors is increased.

RED permits a simpler form for the use of a task or routine when the explicit specification of the translation time property would constitute useless redundancy. Thus, in the above example we could write

The header of the deferred unit being replicated by the generic definition states exactly what the use form must be; the user need only look at this line to determine the proper use form. For example, the above generic definition states that

      p(y);

is the legal use form.

Since not all generic parameters need appear in the generic property list, for routines and tasks it is possible to write a generic definition that produces conflicting overloaded definitions. However, the translator can detect this error while processing the generic. For example,

is illegal, since it produces one definition of f for each possible type, but all these definitions have the same signature (INT). To avoid such an error, it is only necessary to ensure that each formal generic parameter is referenced either as a translation-time property or as part of the type or subtype of a parameter of the routine or task.

Translation-time property lists can be used in defining routines and tasks outside of generic definitions. This is useful when different bodies are needed depending on the return type (for example, in conversion routines). The selection rules for overloaded definitions produced by a generic definition are the same as for explicitly overloaded definitions. The conflict rules are also the same. Thus overloading is treated uniformly, whether produced by explicit or generic definitions.

8.2.3  CONSTRAINT CLAUSES

Parameters to generics can be routines, tasks, types, subtypes, and manifest expressions. In the sections below, the} different kinds of parameters are discussed.

Routines and Tasks

In accordance with Steelman (SM 12D), routines and tasks can be generic parameters. Each formal generic parameter constrained to be a routine or task must be specified with complete information about the types (or subtypes) of its formal parameters. As mentioned above, such a specification serves two purposes: it constrains the actual generic parameter that can be used to instantiate the generic, and it limits use of a routine or task parameter in the body of the generic to be consistent with its specification. Thus we guarantee that in any instantiation the invocation of the actual task or routine will be type-correct.

In specifying the actual routine or task parameter, the user supplies its name and actual translation—time properties (if any). This information must unambiguously select a routine or task definition. That definition is then used in selecting (and possibly creating, as explained above) the appropriate instantiation.

Types

RED permits types to be generic parameters. Usually type generic parameters will be used to stand for any arbitrary type, but forms are also provided to require that the type generic parameter be limited to one of a number of listed types, or to be a type from a particular category (e.g., enumeration).

The NEEDS List

When a generic definition is written based on a type generic parameter, then its body must be defined when any legal actual type is bound to that parameter. However, for the generic definition to have its intended effect, it sometimes needs to invoke routines that operate on data of that type. The NEEDS list, similar to mechanisms found in CLU and Alphard, is provided to state such a requirement.

For example, consider a sort routine that works on arrays of arbitrary component type. Such a routine can work only if the type is ordered. Such a need could be stated in RED as follows:

In the body of sort, "<" is used to determine the proper ordering of a.

The NEEDS list constrains both the body of the generic, and the use of the generic. In the body of the generic, tasks and routines listed in the NEEDS list must be used as specified (e.g., "<" must be used as a function that takes in two t's and returns a BOOL). In the use of the generic, there must be routines and tasks defined in the using environment as stated in the NEEDS list. For example, in

      VAR x: ARRAY INT(1..n) OF s;
      sort(x);

the invocation of sort is legal only if there is a function <, defined in the scope of the invocation, that takes two s's and returns a BOOL.

Other mechanisms than the NEEDS list can be used to ensure that the proper routines and tasks are made available to the generic instantiation. An obvious one is to simply add the needed routines and tasks as additional generic parameters, e.g.,

Such an approach would make generics harder to use, since the need for such routines is very common. For example, a set data abstraction is only defined for elements whose type provides an equality operation. If needed routines had to be passed explicitly, then most set operations would have such a parameter.

At first glance, it may appear that a NEEDS list (or explicit parameters) is totally unnecessary: why can't the translator figure out what is needed?

Essentially, the NEEDS list and generic formal parameters specify all the names that are to be bound in the using environment. An alternative method would be to attach the local meaning to a name that can be used in a generic definition, whenever the name is not a formal generic parameter and has a meaning in the definition scope. Any names left over would then be bound in the using environment. For example, in the function invocation

      x < y

in the sort procedure, where x and y are of type t, "<" must be defined in the using environment; it cannot possibly have a local meaning, since the actual value of t is not known locally.

A deeper analysis shows that such an approach does not work. For example, consider

Obviously, h must be defined in the using environment, since it depends on the actual value of type t. The problem is what to do about g. Suppose there is a local definition of FUNC g(INT) => INT. If in the using environment, h refers to a FUNC(t) => INT, then this local g should be used. However, if h refers to a FUNC(t) => t, then a non-local g must be used.

Such problems make things difficult for the translator. They also make it difficult for the definer of a generic to control its meaning, and for a user to know what a legal instantiation is. As a result, the NEEDS list is the better approach.

The NEEDS list affects the selection (and construction) of an instantiation; it also determines whether the instantiation may legally be used; its use is legal only if routines and tasks as stated in the NEEDS list are available in the using scope.

8.2.4  SUBTYPES

Type generic parameters are useful for the definition of generalized procedures and functions that work for actual parameters of any type (subject to the constraints imposed by the NEEDS list, if any). However, sometimes a generic definition must be specific about subtypes. For example, consider the following

1. a generic type definition

         TYPE t[s] (n: INT) : ARRAY INT(1..n) OF s;

2. a generalized search routine

         FUNC search (a: ARRAY INT OF t, x: t) => INT;

3. a conversion routine

         FUNC convert [t] (s: STRING[ASCII]) => t;

In case 1, the user of t must supply a subtype for s, since s is used as a subtype in defining t. However, it is desirable that the user be informed of what to supply without looking at the definition of t. In case 2, the definer of search may wish to require that the subtype of x be the same as the subtype of elements of a. In example 3, it may be necessary to let the user of convert specify the subtype of the result.

In all three cases, some means of writing a generic definition in terms of subtypes is needed.

RED satisfies these requirements by allowing subtype generic parameters. A subtype generic parameter provides a name that stands for a subtype in the body of the generic; it also constrains the user to explicitly provide a subtype (cases 1 and 3 above) or to satisfy a relationship among subtypes (case 2 above).

The subtype facility can be used to express each of the three examples above:

1. a generic type definition

   

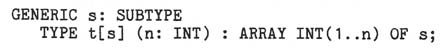
2. a generalized search routine

   

3. a conversion routine from strings to complex numbers

   

A subtype generic parameter does not, however, affect instantiation. A generic definition with a subtype formal parameter stands for all instantiations by type values. Thus, definition (1) above stands for all types t[r], where r is some type. When such a generic is used, i.e.,

      t[u]

where u is a subtype, the type of the subtype (e.g., the type of u) is used to select (and possibly construct) the instantiation. However, the use is legal only if subtype constraints have been satisfied. For example, suppose u and v are different subtypes of the same type. If the user declares

      VAR a: ARRAY INT(1..100) OF u;
      VAR x: u;
      VAR y: v;

then

      search(a,x)
      search(a,y)

both select the same instantiation, but search(a,x) is legal while search(a,Y) is not.

Other methods of describing the need for subtype information were considered and rejected in the design of RED. Essentially there are two other choices:

1. let the context determine whether a type or a subtype is required

2. use assertions to state such information

The main objection to approach 1 is that it is necessary to examine the body of the generic (or possibly some other generic used by the body) to determine whether a type or subtype is needed; such a determination can be arbitrarily difficult for the user to make. Furthermore, this approach is not sufficient to express example 2 above, since either types or subtypes can be specified in routine headers.

The second alternative is similar to what we have. Our method is superior because it permits a more succinct statement of requirements, and because it is more obvious when a name stands for a subtype.




8.2.5  MANIFEST EXPRESSIONS

A generic parameter can stand for a manifest expression, in accordance with Steelman (SM 12D). Since the actual parameters must be manifest, optimizations can be performed on the instantiations. Therefore, such parameters are useful in writing generalized packages that permit instantiations.

For example, a library of mathematical functions can be parameterized by precision, and then instantiations created for standard precisions, and the instantiations optimized for these cases.




8.2.6  IMPLEMENTATION



The main implementation issue with generics concerns instantiation. when the need for an instantiation is discovered, the translator is processing a program that uses the generic. However, the generic must be instantiated in its definition environment, with the formal generic parameters bound to the actual values (and needed operations, if any, bound to the actual needed routines). Thus to process the instantiation, the translator must shift from the environment of the use to the definition environment of the generic. This shift might be done immediately (i.e., the translator invokes itself recursively when it needs an instantiation) or delayed until after the using program has been processed.

A reasonable way to accommodate the shift in environment is to collect information about the environment of a generic definition when it is processed. The translator must process a generic definition to determine if it is legal; basically, this legality checking determines that the formal generic parameters are used appropriately, and that the definition environment provides required definitions. During this processing, information about the generic parameters (and the NEEDS list, if any) and the definition environment would naturally be collected in some sort of symbol table. All that need be done is to save this symbol table in the program library along with the source for the generic. Then instantiation consists of filling in information about the actual generic parameters (and routines and tasks named in the NEEDS list) in the symbol table of the generic, and then translating the source of the body of the generic in the context of that symbol table. During this translation, optimizations can be done based on the values of the actual generic constraints.

Generics are defined in such a way that it is irrelevant how often an instantiation is produced: the meaning of a program is the same if an instantiation is constructed just once, and all uses refer to it (i.e., all share the code) or if each use causes the instantiation to be constructed again (no sharing of code), or anything in between. This flexibility is important because it permits the A translator to optimize the code produced to save space or time as desired. For example, inline substitution of the instantiation provides time efficiency at the expense of space, while sharing the code saves space but costs time.

To avoid constructing an instantiation more than once (if this is desired), it is necessary to remember an instantiation that has been constructed previously, and then reuse that instantiation. This can be done because every instantiation has a unique name that is known at translation time. The name consists of the identifier naming the deferred unit that is the body of the generic, the actual values of all the translation-time parameters (including implicit parameters acquired via the NEEDS list), and the signature (if any). This name can be produced from any legal use of an instantiation, and therefore can be used to store and later fetch the code of the instantiation. The instantiation might be remembered just for the translation of a single module, or it might be remembered for much longer by storing the instantiation and its name in the program library.

It is possible to have more of the work of producing an instantiation done at the time the generic definition is processed. In many cases almost all object code can be produced at this time. The output of the translator would consists of two parts: the object code, and some generic-parameter-dependent information. Then an instantiation can be produced in one of two ways:

1. Using the actual generic constraints and the parameter-dependent information, the translator copies the object code and modifies it appropriately to produce the code for the instantiation.

2. The parameter-dependent information is copied and the values of the actual generic constraints are filled in. The instantiation shares the object code with other instantiations.

The object code will refer to generic constraint information for the appropriate instantiation via a pointer in the activation record.

For example, consider the integrate routine discussed earlier. This could be preprocessed, and complete object code generated except for the invocations of the function that is its generic argument. (Separate code bodies could be produced for the four combinations of single-precision/double-precision actual parameters.) The function invocations could be handled by leaving blanks in the object code, and having the parameter-dependent information state where the blanks are (such information would be analogous to the link table in a linking loader); then instantiation would make a new copy with the blanks filled in. Alternatively, instantiation could be done by creating a new parameter-dependent part; the instantiations could all share the object code, and access parameter values indirectly. This second alternative may be the more desirable since the time penalty for the indirect invocation is slight and the space savings is large.

Thus, generics in RED provide flexibility in optimization for space or time through a variety of implementation techniques. Many of these techniques are based on existing work in the CLU implementation [ALS78] and also the Alphard implementation. For example, the CLU implementation uses a code sharing technique similar to the one sketched above.